Contoh soal fungsi kuadrat matematika ekonomi dan jawabannya – Kali ini sobat PenaGuru akan membagikan latihan dan contoh soal fungsi kuadrat matematika. Sub materi yang akan dibahas berkaitan dengan matematika ekonomi. Jadi silahkan simak penjelasan mengenai contoh soal fungsi kuadrat dan pembahasannya berikut ini.
Contoh soal fungsi kuadrat kelas 10 ini akan memudahkan peserta didik dalam menguasai materi fungsi kuadrat. Selain itu, dapat menjadi soal dalam penilaian harian dan PTS maupun PAS kelas 10 SMA.
Contoh Soal Fungsi Kuadrat Matematika Ekonomi dan Jawabannya
Langsung saja pelajari contoh soal fungsi kuadrat matematika ekonomi dan jawabannya dalam bentuk pilihan ganda di bawah ini.
Pilihlah salah satu jawaban yang menurut Anda paling tepat!
1. Identifikasilah grafik fungsi logaritma f(x) = ln (-x)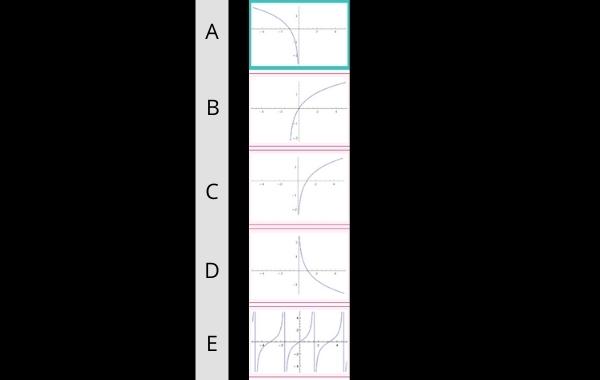
Petunjuk:
Untuk mencari titik potong dengan sumbu X, selesaikanlah persamaaan berikut ini :f(x) = ln (-x) = 0
Pembahasan:
Asimptot vertikal diperoleh dengan menyelesaikan
-x = 0 (karena ln(0+) menuju negatif tak hingga)
atau
x = 0
Dengan demikian, asimptot vertikal adalah pada x = 0.
Selanjutnya, untuk mencari titik potong dengan sumbu X, kita harus menyelesaikan persamaan berikut ini :
f(x) = 0
ln(-x ) = 0
eln(-x) = e0
-x = 1
x = -1
Dengan demikian, titik potong dengan sumbu X adalah (-1 , 0).
Sedangkan untuk mencari titik potong dengan sumbu Y, kita harus menghitung nilai dari f(0). Akan tetapi, karena ln(0) tidak ada, maka titik potong antara f(x) dan sumbu Y tidak ada.
Jadi, grafik yang benar adalah yang mempunyai x = -1 sebagai absis titik potong dengan sumbu X, mempunyai asimptot vertikal pada x=0, dan tidak pernah memotong sumbu Y.
2. Identifikasilah grafik fungsi eksponensial f(x) = e (x + 2)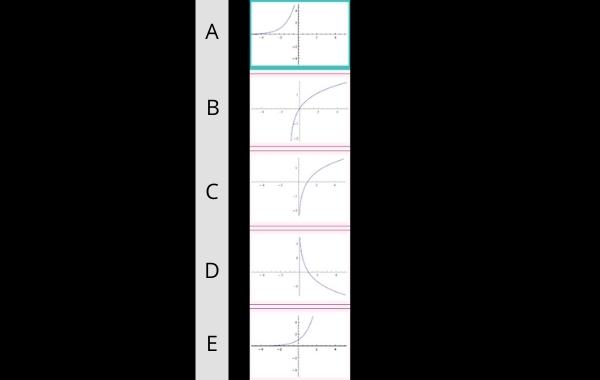
Petunjuk:
Titik potong dengan sumbu X diperoleh dengan menyelesaikan persamaan f(x) = e (x + 2) = 0
yang mana tidak akan pernah bernilai nol. Dengan demikian, titik potong dengan sumbu X tidak ada.
Pembahasan:
Titik potong dengan sumbu X diperoleh dengan menyelesaikan persamaan f(x) = e (x + 2) = 0
yang mana tidak akan pernah bernilai nol. Dengan demikian, titik potong dengan sumbu X tidak ada. Adapun fungsi tersebut hanya mendekati 0 pada negatif tak hingga, tetapi tidak pernah memotong sumbu X.
Sedangkan titik potong fungsi dengan sumbu Y adalah :
f(x) = e (x + 2) = e2 = 7.389
Selain itu, karena e0 = 1 = e (x + 2)
maka f(-2) = 1.
3. Dari grafik berikut ini, manakah yang merepresentasikan fungsi eksponensial f(x) = -e -x ?
Petunjuk:
Titik potong dengan sumbu Y adalah :
f(x) = -e -x = -e0 = -2.7183
Titik potong dengan sumbu X dapat dicari dengan menyelesaikan f(x) = -e -x = 0
Pembahasan:
Titik potong dengan sumbu X diperoleh dengan menyelesaikan persamaan f(x) = e (x + 2) = 0
yang mana tidak akan pernah bernilai nol. Dengan demikian, titik potong dengan sumbu X tidak ada. Adapun fungsi tersebut hanya mendekati 0 pada negatif tak hingga, tetapi tidak pernah memotong sumbu X.
Sedangkan titik potong fungsi dengan sumbu Y adalah :
f(x) = -e -x = -e0 = -2,7183
Fungsi ini akan lebih bernilai negatif di sepanjang sumbu X. Hal ini dikarenakan pangkat (-x) naik dan -e-x menjadi semakin bernilai negatif.
4. Dari grafik berikut ini, manakah yang merepresentasikan fungsi logaritma f(x) = ln (x – 1) + 1?
Petunjuk:
Untuk mencari titik potong dengan sumbu X, selesaikanlah persamaan : f(x) = ln (x – 1) + 1 = 0
Sedangkan untuk mencari titik potong dengan sumbu Y, hitunglah nilai dari f(0).
Pembahasan:
Asimptot vertikal dapat diperoleh dengan cara menyelesaikan
x – 1 = 0 (Karena ln(0+) menuju negatif tak hingga)
atau
x = 1
Untuk mencari titik potong dengan sumbu X, kita harus menyelesaikan persamaan :
f(x) = 0
ln(x – 1) +1 = 0
ln(x – 1) = -1
Selanjutnya, dengan menggunakan sifat fungsi logaritma dan eksponensial, kita dapat menulis persamaan di atas menjadi :
eln(x – 1) = e-1
dengan melakukan penyederhanaan,
x – 1 = e-1
x = e-1 + 1 ≈ 1.37
Jadi, titik potong dengan sumbu X adalah (1,37 ; 0).
Sedangkan untuk mencari titik potong dengan sumbu Y, kita harus menghitung nilai dari f(0). Akan tetapi, karena ln(0-1) = ln(-1) tidak ada, maka titik potong antara f(x) dan sumbu Y tidak ada.
Oleh karena itu, grafik yang benar adalah grafik dengan absis titik potong pada sumbu X adalah 1,37 ; mempunyai asimptot vertikal pada x=1 ; dan tidak berpotongan dengan sumbu Y.
5. Identifikasilah grafik fungsi logaritma berikut ini : f(x) = -ln (-x + 1)
Petunjuk:
Untuk mencari titik potong dengan sumbu X, kita harus menyelesaikan persamaan f(x) = -ln (-x + 1) = 0
Perhatikan bahwa nilai f(x) semakin bernilai negatif di sepanjang sumbu X negatif.
ln (2) = 0,69
Pembahasan:
Asimptot vertikal diperoleh dengan cara menyelesaikan
– x + 1 = 0
atau
x = 1
Untuk mencari titik potong dengan sumbu X, kita harus menyelesaikan persamaan :
f(x) = 0
-ln(-x + 1) = 0
ln(-x + 1) = 0
Selanjutnya, dengan menggunakan sifat fungsi logaritma dan eksponensial, persamaan di atas dapat ditulis menjadi :
eln(-x + 1) = e0
dengan menyederhanakan, diperoleh :
-x + 1 = 1
x = 0
Dengan demikian, titik potong dengan sumbu X adalah (0 , 0). Adapun titik tersebut juga merupakan titik potong f(x) dengan sumbu Y.
Selanjutnya, karena nilai x semakin negatif, maka ln(-x+1) nilainya naik, namun f(x) = -ln(-x+1) nilainya semakin menurun.
Jadi, jawaban yang benar adalah grafik yang melalui titik asal, mempunyai asimptot vertikal pada x=1, dan bernilai semakin negatif di sepanjang sumbu X negatif.
6. Fungsi eksponensial f(x) = -e (-x – 1) + 1 direpresentasikan oleh grafik berikut ini :
Petunjuk:
Carilah absis dari titik potong fungsi dengan sumbu X dengan menyelesaikan f(x) = 0.
Pembahasan:
Absis titik potong dengan sumbu X dapat dicari dengan menyelesaikan
f(x) = -e (-x – 1) +1 = 0
e (-x – 1) = 1 = e0
dengan membandingkan pangkat, diperoleh :
-x-1 = 0
atau
x = -1
Ordinat titik potong dengan sumbu Y adalah :f(0) = -e (-x – 1) +1 = -e-1 +1 = 0,632
Dengan demikian, hanya ada satu grafik dalam pilihan jawaban, dimana absis titik potong dengan sumbu X adalah -1. Jadi, grafik tersebut adalah jawaban yang benar.
7. Dari grafik berikut ini, manakah yang merepresentasikan f(x), jika diketahui :f (x) = -3 ln (x – 4)
Petunjuk:
Untuk mencari titik potong dengan sumbu X, selesaikanlah persamaan : f(x) = 0
Selanjutnya, jika x naik, maka ln(x-4) naik, tetapi f(x)= -3 ln(x-4) menjadi semakin bernilai negatif.
Pembahasan:
Asimptot vertikal diperoleh dengan menyelesaikan
x – 4 = 0
or
x = 4
Untuk mencari absis titik potong dengan sumbu X, kita harus menyelesaikan persamaan :
f(x) = 0
-3ln(x – 4) = 0
Selanjutnya, dengan membagi kedua ruas dengan -3, diperoleh :
ln(x – 4) = 0
Dengan menggunakan sifat fungsi logaritma dan eksponensial,
kita dapat menulis persamaan di atas menjadi :
eln(x – 4) = e0
Then simplify
x – 4 = 1
x = 5
Jadi, titik potong dengan sumbu X adalah (5 , 0).
Titik potong dengan sumbu Y adalah (0 , f(0)). Oleh karena x=0 bukan merupakan domain dari f, maka f(0) tidak terdefinisi. Jadi, tidak ada titik potong dengan sumbu Y.
Selanjutnya, jika x naik, maka ln(x-4) naik, tetapi f(x)=-3 ln(x-4) menjadi semakin bernilai negatif.
Dengan demikian, hanya ada satu grafik yang memenuhi semua kondisi tersebut.
8. Dari pilihan di bawah ini, grafik manakah yang merepresentasikan f(x) f(x) jika diketahui : f (x) = 3(x + 1) – 2?
Petunjuk:
Untuk mencari titik potong dengan sumbu X, maka kita harus menyelesaikan persamaan f(x) = 0
Jika nilai x menurun tanpa batas, maka f(x) = 3(x + 1) -2 mendekati -2.
Pembahasan:
Jika x menurun tanpa batas, maka f(x) = 3(x + 1) -2 mendekati -2. Grafik fungsi f mempunyai asimptot horizontal y = -2.
Untuk mencari nilai dari absis titik potong dengan sumbu X, kita harus menyelesaikan persamaan :
f(x) = 0
3(x + 1) – 2 = 0
Dengan menambahkan 2 kedalam kedua ruas persamaan, diperoleh : 3(x + 1) = 2
Dengan menuliskan kembali persamaan di atas dalam bentuk logaritma, diperoleh : x +1 = log3 2
Dengan menyelesaikan nilai x, diperoleh : x = log3 2 – 1 = -0.369
Titik potong dengan sumbu Y adalah (0 , f(0)) = (0 , 3(0 + 1) – 2) = (0 ,1).
9. Dari pilihan berikut ini, fungsi manakah yang merepresentasikan grafik di bawah ini?
A. f(x) = 2 ln |x|
B. f(x) = ln |x|
C. f(x) = ln x
D. f(x) = e|x|
Petunjuk:
ln 4= 1.3863 , e4 = 54,6
Pembahasan:
Karena absis titik potong dengan sumbu X adalah x = 1, -1 ; maka f(1)=0 dan f(-1)=0
Akibatnya, dari pilihan jawaban yang ada, f(x) = e^|x| dan f(x) = |e| tidak memenuhi kondisi di atas, karena nilainya tidak sama dengan nol saat x = 1.
Selain itu, f(x) ≠ ln x karena ln (-1) ≠ 0 (ln(-1) is tidak terdefinisi)
Dari grafik di atas, karena f(4) ≈ 2,6 dan ln(4) = 1,3863 maka f(x) tidak mungkin merupakan ln |x|.
Dengan demikian, jawaban yang benar adalah : f(x) = 2 ln |x|
10. Grafik yang merepresentasikan fungsi f(x) = log2 (x + 2) adalah :
Petunjuk:
Untuk mencari titik potong dengan sumbu X, kita harus menyelesaikan persamaan :
f(x) = 0
log2 (x + 2) = 0
Dengan menggunakan sifat fungsi logaritma dan eksponensial, diperoleh : 2log2 (x + 2) = 20 ekuivalen dengan x+2 = 1 atau x = -1
Pembahasan:
Asimptot vertikal dapat diperoleh dengan menyelesaikan
x + 2 = 0
yang mana memberikan
x = -2
Karena x menuju -2 dari kanan (x > -2), maka f(x) menurun tanpa batas.
Untuk mencari titik potong dengan sumbu X, maka kita harus menyelesaikan persamaan :
f(x) = 0
log2 (x + 2) = 0
Dengan menggunakan sifat fungsi logaritma dan eksponensial, persamaan di atas dapat ditulis menjadi : 2log2 (x + 2) = 20
Dengan melakukan penyederhanaan, diperoleh :
x + 2 = 1
x = -1
Jadi, titik potong dengan sumbu X adalah (-1 , 0).
Titik potong dengan sumbu Y diberikan oleh (0 , f(0)) = (0 , log2 (0 + 2)) = (0 , 1).
Grafik dengan titik potong pada sumbu X adalah (-1,0) dan titik potong dengan sumbu Y adalah (0, 1) merupakan jawaban yang benar.
Itulah contoh soal fungsi kuadrat matematika ekonomi dan jawabannya yang sempat kami bagikan. Semoga bermanfaat buat bapak ibu guru dan peserta didik.



