Contoh Soal Matriks dan Jawabannya Kelas 11 – Halo sahabat Penaguru, pada postingan kali ini, admin akan membagikan contoh soal matematika kelas 11 SMA SMK sederajat. Soal tersebut berkaitan dengan materi matriks. Peserta didik dapat berlatih sendiri mengerjakan soal tersebut di rumah melalui gadget masing-masing.
Selain itu, contoh soal matriks dan jawabannya kelas 11 ini dapat digunakan oleh bapak ibu guru sebagai referensi dalam Menyusun soal penilaian harian maupun ulangan akhir semester atau UAS kelas 11 SMA. Mereka tinggal menyesuaikan dengan kompetensi dasar yang diajarkan di kelas masing-masing.
Contoh Soal Matriks dan Jawabannya Kelas 11 Pilihan Ganda
Silahkan pelajari contoh soal matriks pilihan ganda dan jawabannya kelas 11 beserta dengan pembahasannya berikut ini.
1. Determinan matriks adalah ….
A. suatu skalar kuantitas
B. suatu vektor kuantitas
C. invers dari matriks tersebut
D. matriks kuadrat
E. matriks persegi panjang
Petunjuk:
Pahami tentang pengertian determinan suatu matriks.
Pembahasan:
Perhatikan matriks M, matriks persegi berordo 2 x 2 berikut.
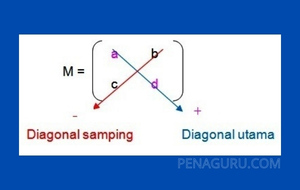
Hasil kali unsur-unsur diagonal utama dikurangi hasil kali unsur-unsur diagonal samping, yaitu ad – bc disebut determinan matriks M, disingkat det M. Perhatikan bahwa a, b, c, dan d merupakan bilangan real sehingga ad – bc juga merupakan bilangan real. Bilangan real merupakan sebuah skalar kuantitas. Jadi, determinan suatu matriks adalah suatu skalar kuantitas.
2. Nilai x yang memenuhi adalah ….

A. x = ± 1
B. x = 4 dan x = 1
C. x = -4 dan x = -1
D. x = ± 4
E. x=1
Petunjuk:
Gunakan rumus berikut ini untuk menghitung determinan dari suatu matriks berukuran 2×2 :

Pembahasan:
Determinan dari matriks berukuran 2×2 adalah sebagai berikut :

Dengan demikian,

3. Dari pilihan berikut ini, operasi manakah yang tidak menggunakan determinan dalam kalkulasinya?
A. Transpos dari suatu matriks
B. Adjoint dari suatu matriks
C. Minor dari sebuah elemen dalam matriks
D. Invers dari suatu matriks
E. Kofaktor dari suatu matriks
Petunjuk:
Ingat kembali semua aplikasi dari determinan suatu matriks.
Pembahasan:
Minor dari elemen aij dalam sebuah matriks dapat dibentuk dengan cara menghitung determinan dari matriks terbentuk dengan cara mengilangkan baris ke-i dan kolom ke-j.
Kofaktor dari sebuah elemen dalam sebuah matriks dapat dibentuk dengan menggunakan minor Mij dari aij yaitu dengan cara memasukkan dan mengaplikasikan persamaan berikut ini :
Untuk menentukan adjoint dari dari sebuah matriks, kita perlu menghitung kofaktor dari matriks tersebut. Adapun untuk menghitung kofaktor, kita perlu menghitung minor, dimana untuk menghitung minor, kita harus tahu nilai determinan dari matriks tersebut.
Invers dari suatu matriks menggunakan adjoint dari matriks, sedangkan untuk menghitung adjoint, kita harus tahu nilai determinan dari matrik tersebut.
4. Dari matriks A dan B berukuran 2×2, evaluasilah bentuk berikut ini :

A. 8
B. 12
C. -8
D. -12
E. -2(6)
Petunjuk:
Pertama-tama, hitunglah nilai determinan A dan B, kemudian sederhanakan persamaan tersebut. 2|A|-7|B|
Pembahasan:
Evaluasilah determinan dari kedua matriks dan gunakan langkah berikut ini untuk memperoleh penyelesaian.

5. Dari pilihan berikut ini, matriks manakah yang mempunyai determinan yang berbeda dengan matriks berikut ini?


Petunjuk:
Ingat kembali pengaruh penukaran 2 baris atau 2 kolom terhadap nilai dari determinan suatu matriks dengan ukuran 3×3.
Pembahasan:
Untuk menyelesaikan soal di atas, kita dapat menggunakan sifat determinan suatu matriks : “Jika setiap dua baris atau kolom ditukar posisinya, maka determinan dari matriks yang terbentuk adalah negatif dari determinan matriks awal”.
6. Determinan dari matriks berikut ini adalah ….
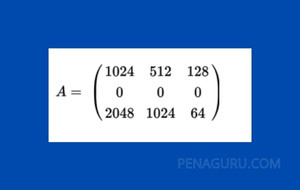
A. 0
B. 33.554.432
C. 134.217.728
D. 67.108.864
E. 1
Petunjuk:
Gunakan rumus berikut ini untuk menghitung nilai determinan dari matriks berukuran (m x n)
Dalam hal ini, m=n=3

Pembahasan:
Untuk menyelesaikan soal di atas, kita dapat menggunakan sifat determinan suatu matriks : “Jika sebarang baris atau kolom dalam suatu matriks adalah nol, maka determinan dari matriks tersebut juga sama dengan nol”.
7. Nilai x yang memenuhi persamaan berikut ini adalah ….

A. -2,3
B. 2,-3
C. 2,2
D. 3,3
E. √2,-3
Petunjuk:
Gunakan rumus berikut ini untuk menghitung determinan dan menyelesaikan persamaan kuadrat, yaitu dengan menjabarkan nilai determinan dari matriks berukuran 3×3 yang telah diberikan.
Pembahasan:
Pertama-tama, kita akan mencari nilai determinan dari matriks berukuran 3×3, kemudian kita akan mencari nilai x dengan terlebih dahulu mencari penyelesaian dari persamaan kuadrat.

8. Determinan dari matriks berikut ini adalah ….

A. 0
B. 1024
C. 99
D. 1
E. 12234
Petunjuk:
Sederhanakan bentuk akar yang ada, kemudian hitung nilai determinan dari matriks di atas dengan menggunkan rumus berikut ini :

Pembahasan:
Akar pangkat enam dari 729 adalah 3, akar pangkat lima dari 1024 adalah 4, dan akar pangkat empat dari 625 adalah 5. Selanjutnya, kita akan menjabarkan determinan tersebut untuk memperoleh jawaban yang dicari.
9. Nilai x dan y yang memenuhi sistem persamaan berikut ini adalah….

A. x = 2, y = 1
B. x = -2, y = -1
C. x = -2, y = 1
D. x = , y = -1
E. x = 0, y = 0
Petunjuk:
Bentuklah dua persamaan dengan terlebih dahulu menghitung nilai determinan dari kedua matriks, kemudian menyelesaikannya secara simultan.

Pembahasan:
Dengan terlebih dahulu menghitung nilai determinan dari kedua matriks dan menyelesaikannya secara simultan, dapat dibentuk dua persamaan.
Berikut ini adalah penyelesaian dari permasalahan di atas :
10. Determinan dari matriks berukuran 4×4 berikut ini adalah….

A. -48
B. 48
C. 68
D. -68
E. 1
Petunjuk:
Gunakan ekspansi kolom pertama hingga diperoleh matriks 3 x 3, selanjutnya gunakan ekspansi baris pertama untuk mencari determinan dari matriks 3 x 3 tersebut.

Pembahasan:
Nilai determinan dari matriks 4 x 4 dapat dicari dengan menggunakan metode ekspansi kolom pertama hingga diperoleh matriks 3 x 3, selanjutnya dapat digunakan ekspansi baris pertama untuk mencari determinan dari matriks 3 x 3 tersebut.
Demikian Contoh Soal Matriks dan Jawabannya Kelas 11 yang dapat kami bagikan kali ini. Semoga bermanfaat dalam pembelajaran matematika SMA kelas 11, khususnya kompetensi dasar yang memuat materi tentang matriks.



